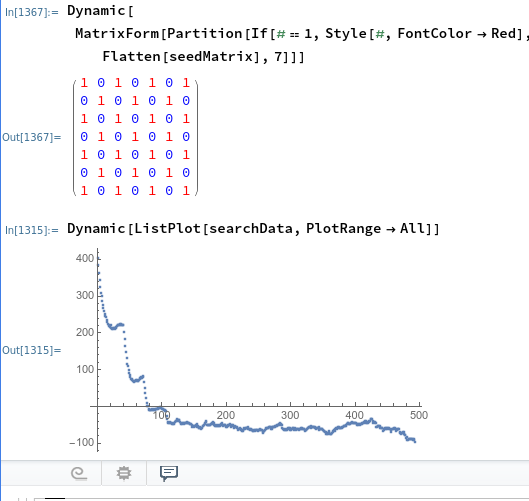
Modelling a Magnetic Cube: Dipoles!

So I found this paper https://doi.org/10.1063/1.4941750 (It's open access by the way) and in it they have a nice equation for the energy between two magnetic dipoles. $$E_{m_{1}m_{2}} = \frac{1}{4\pi\mu}\frac{m_{1}m_{2}-3(m_{1}e_{r})(m_{2}e_{r})}{|l^{3}|}$$ In it, the terms m1 and m2 describe the dipole vector of each magnet, and er describes the normal vector between the centers of each dipole, l describes the distance between the two dipoles, and mu is the permeability of the medium. For our purposes I got rid of mu because it's just a scaling factor. With dipoles the determination of the energy becomes a little more complicated because I've got to permute through all the possible orientations of the magnets in order to find the best choice for moving to a lower energy. This is simplified greatly by the fact that the magnets in this case are cubes and so can only have six possible orientations. In the code I've described this with an integer (1 to 6...